그래프
: 연결되어 있는 원소 사이의 다:다 관계를 표현하는 자료구조 ( 트리는 1:N 관계 표현 )
그래프 G = 객체를 나타내는 정점(Vertex)과 객체를 연결하는 간선(Edge)의 집합. G = (V, E)
그래프의 종류

무방향 그래프
: ( = 양방향 그래프) 두 정점을 연결하는 간선에 방향이 없는 그래프, 정점 Vi와 정점 Vj를 연결하는 간선을 (Vi, Vj)로 표현
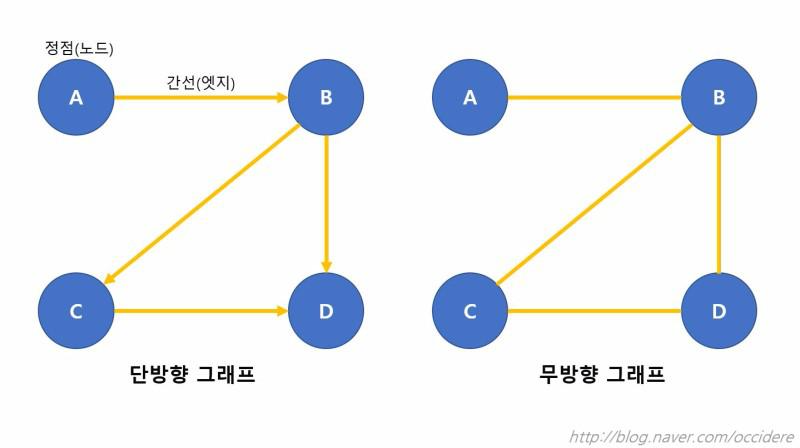
ex) 위 그림의 왼쪽 그래프가 G1, 오른쪽 그래프가 G2일 때. V(G2) = (A, B, C, D). E(G2) = {(A, B), (B, C), (B, D), (C, D)}
방향 그래프
: 간선에 방향이 있는 그래프, 정점 Vi에서 정점 Vj를 연결하는 간선 즉, Vi -> Vj를 <Vi, Vj>로 표현. Vi를 꼬리(tail), Vj를 머리(head)라고 한다. <Vi, Vj> 와 <Vj, Vi>는 서로 다른 간선을 의미.
ex) V(G1) = (A, B, C, D). E(G1) = {<A, B>, <B, C>, <B, D>, <C, D>}
완전 그래프
: 각 정점에서 다른 모든 정점을 연결하여 최대로 많은 간선 수를 가진 그래프
정점이 n개인 무방향 그래프에서 최대의 간선 수 : n(n-1)/2개
정점이 n개인 방향 그래프의 최대 간선 수 : n(n-1)개
부분 그래프
: 원래의 그래프에서 정점이나 간선을 일부만 제외하여 만든 그래프. 그래프 G와 G'의 관계. V(G')는 V(G)의 부분집합, E(G')는 E(G)의 부분집합.
가중 그래프, 네트워크
: 정점을 연결하는 간선에 가중치(weight)를 할당한 그래프.
ex) 아래 그래프를 예시로 정점이 장소, 가중치가 시간일 때 A에서 B까지 가는데 걸리는 시간은 30.
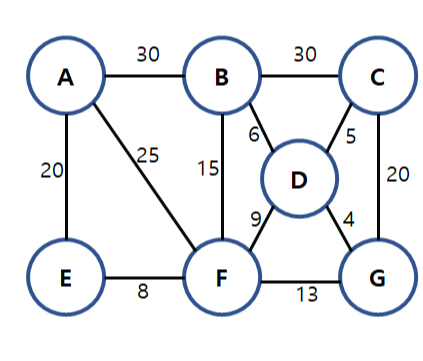
그래프 관련 용어
그래프에서 두 정점 Vi와 Vj를 연결하는 간선(Vi, Vj)가 있을 때, 두 정점 Vi와 Vj를 인접(adjacent)되어 있다고 하고, 간선 (Vi, Vj)는 정점 Vi와 Vj에 부속(incident)되어 있다고 함.
ex) 위 그래프에서 정점 D와 인접한 정점은 C와 B이고, 정점 D에 부속되어 있는 간선은 (D, C)와 (D, B).
차수
: 정점에 부속되어 있는 간선의 수
ex) 위 무방향 그래프에서 A의 차수는 1, B의 차수는 3, C의 차수는 2이다. 단방향 그래프의 차수는 정점을 머리로 하는 간선 수인 진입차수와 정점을 꼬리로 하는 간선 수인 진출차수의 합이다. 정점 B의 진입 차수는 <A, B>로 1개, 진출차수는 <B, C>, <B, D>로 2개 총 3개이다.
경로
: 그래프에서 간선을 따라 갈 수 있는 길을 순서대로 나열한 것 즉, 정점 Vi에서 정점 Vj까지 간선으로 연결된 정점을 순서대로 나열한 리스트. 경로 길이 = 경로를 구성하는 간선의 수.
ex) 위 무방향 그래프에서 정점 A에서 정점 C까지 가는 경로는 A-B-C, A-B-D-C 총 2개.
단순 경로 :
- 모두 다른 정점으로 구성된 경로.
- ex) 위 무방향 그래프에서 정점 D에서 정점 A까지 가는 경로 중 D-B-A는 단순 경로이지만, D-B-C-D-B-A는 단순 경로가 아님.(후자도 경로라고 할 수 있지만 잘 안 쓰인다.)
사이클
- : 단순 경로 중에서 경로의 시작 정점과 마지막 정점이 같은 경로.
- ex) 위 무방향 그래프의 경로 중 D-B-D 또는 A-B-C-B-A는 사이클.
DAG
- : 방향 그래프이면서 사이클이 없는 그래프
연결 그래프
- : 서로 다른 모든 쌍의 정점들 사이에 경로가 있는 그래프. 즉, 떨어져 있는 정점이 없는 그래프.
- 그래프에서 두 정점 사이에 경로가 있다면 두 정점은 연결되었다고 함. 트리는 사이클이 없는 연결 그래프. (정점이 n개 일 때 트리의 간선 수는 n-1개이다. 간선 수가 n-1개 이상이 되면 사이클이 생기므로 트리가 아님.)
단절 그래프
- : 연결되지 않은 정점이 있는 그래프.
트리에 대한 설명글은 여기 👇🏻
https://tildacoderecorder.tistory.com/104
[ 자료구조 ] 트리와 이진트리의 개념과 구조 - C언어
트리 Tree 트리 : 원소들 간에 1:n 관계를 가지는 비선형 자료구조, 원소들 간에 계층 관계를 가지는 계층형 자료구조, 상위 원소에서 하위 원소로 내려가면서 확장되는 트리(나무) 모양의 구조 트
tildacoderecorder.tistory.com
참고 : C로 배우는 쉬운 자료구조 / 이지영 / 한빛아카데미
'C' 카테고리의 다른 글
| Union-Find 알고리즘 (동치류 문제) / 크루스칼 알고리즘 - C 언어 (0) | 2021.06.11 |
|---|---|
| 신장 트리 / 최소 비용 신장 트리 / 프림 알고리즘, 크루스칼 알고리즘 - C 언어 (0) | 2021.06.10 |
| heap의 개념과 구조, 삽입/삭제 연산 - C언어 (0) | 2021.06.01 |
| 이진 탐색 트리의 탐색/삽입/삭제 연산 - C언어 (1) | 2021.05.30 |
| 트리와 이진트리의 개념과 구조 - C언어 (0) | 2021.05.28 |