Heap
: 완전 이진 트리에 있는 노드 중에서 키 값이 가장 큰 노드나 키 값이 가장 작은 노드를 찾기 위해 만들어진 자료 구조
최대 히프 max heap
: 키 값이 가장 큰 노드를 찾기 위한 완전 이진 트리, 부모 노드의 키 값 >= 자식 노드의 키 값, 루트 노드 : 키 값이 가장 큰 노드
최소 히프 min heap
: 키 값이 가장 작은 노드를 찾기 위한 완전 이진 트리, 부모 노드의 키 값 <= 자식 노드의 키 값, 루트 노드 : 키 값이 가장 작은 노드
❗️ 이진 트리에서는 왼쪽이 루트 노드보다 작고 오른쪽이 루트 노드보다 컸지만 히프는 좌우가 아닌 상하를 따짐.
히프의 구현

1차원 배열의 순차구조를 이용하면 인덱스 관계를 이용하여 부모 노드를 찾을 수 있다. 위에서 아래로 내려오면서 동시에 왼쪽부터 차례대로 배열의 원소가 된다. ( 인덱스 0은 사용하지 않는다 )
- 부모 노드의 인덱스 = 인덱스/2
- 왼쪽 자식 노드의 인덱스 = 인덱스*2
- 오른쪽 자식 노드의 인덱스 = 인덱스*2+1
위 그림을 예시로 들 때 인덱스가 3이고 원소가 B인 노드의 부모 노드는 3/2 = 1 ( 나머지는 생략 )이므로 인덱스가 1인 A이다.
B의 자식노드는 각각 F와 K인데 이를 1차원 배열에서 찾는다면, 왼쪽 자식 노드는 3^2 = 6 이므로 인덱스가 6인 F가 나오고, 오른쪽 자식 노드는 3^2+1 = 7이므로 인덱스가 7인 K가 잘 나오는 것을 확인할 수 있다.
이렇게 1차원 배열을 이용하여 히프의 삽입과 삭제 연산을 구현할 수 있다.
히프의 기본 구조
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
#include <stdio.h>
#include <stdlib.h>
#define MAX_ELEMENT 100
//히프에 대한 1차원 배열과 히프 원소의 갯수를 구조체로 묶어 선언
typedef struct {
int heap[MAX_ELEMENT];
int heap_size;
} heapType;
heapType *createHeap() { //공백 히프를 생성하는 연산
heapType *h = (heapType*)malloc(sizeof(heapType));
h->heap_size = 0;
return h;
}
|
cs |
구조체 heapType에 크기가 100인 1차원 배열 heap와 히프의 원소 갯수를 나타내는 heap_size를 선언한다.
공백 히프 h를 생성하고 공백이기 때문에 heap_size에 0을 넣어준다.
최대 Heap 삽입 연산
: 히프에 새로운 원소를 삽입할 때는 두 단계를 거친다. 먼저 완전 이진 트리의 조건이 만족하도록 새 노드를 만들고 그 자리에 삽입할 원소를 저장한다. 그 후, 부모 노드와 크기 비교하여 알맞은 원소의 위치가 될 때 까지 이동한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
void insertHeap(heapType *h, int item) {
int i;
h->heap_size = h->heap_size + 1;
i = h->heap_size;
while ( (i != 1)&& (item > h->heap[i/2])) {
h->heap[i] = h->heap[i/2];
i /=2;
}
h->heap[i] = item;
}
|
cs |
파라미터로 히프 h와 삽입할 원소 item을 받는다. 부모 노드와의 크기 비교를 통해 item이 들어갈 알맞은 위치를 찾는 용도로 정수형 변수 i를 선언한다.
원소를 하나 새로 삽입하기 때문의 히프의 원소 개수를 1 증가시켜야 한다. 따라서 h->heap_size = h->heap_size + 1를 해주고, i에 heap_size를 담아준다.
while문은 부모 노드와의 크기 비교를 해 위치를 바꾸는 반복문이다. 조건문을 보자면, i가 1이면 루트 노드이기 때문에 비교할 필요가 없어 종료해야 하고, item이 h->heap[i/2], 즉 부모 노드 보다 작으면 이동하지 않아도 되므로 반복문을 종료한다.
위 반복문을 종료한 뒤에는 인덱스 i의 자리에 item 값을 넣어준다.
이를 그림으로 보자면, 위 트리는 노드가 9개인 완전 이진 트리이다. 새로 삽입할 item은 18이라고 할 때, 위 코드의 순서를 그대로 따라가보자. heap_size에는 9가 들어가 있지만 새 노드를 삽입하므로 1을 더 한 10이 들어간다. i에도 heap_size인 10이 담긴다.
반복문의 조건을 볼 때, 10은 1이 아니기 때문에 첫번째 조건은 통과하지만 두번째 조건인 item > h->heap[i/2]은 통과하지 못 한다. 부모 노드는 10/2이고, 이는 위 트리에서 29를 가리키는데 새로 삽입할 원소 18은 29보다 작기 때문이다.
그래서 반복문을 돌지 못 하고 바로 다음 코드로 넘어간다. 배열의 10번째 노드가 18이 된다. 즉, 29의 왼쪽 자식 노드가 되는 것이다.
만약 새로 삽입할 원소가 18이 아닌 31이라면 반복문에 들어갔을 때 부모 노드인 29보다 크기 때문에 while문을 돌게된다.
h->heap[i] = h->heap[i/2]로 배열의 10번째 자리에 부모 노드인 29가 들어가고, i/2를 하면 5. 반복문을 한번 돌아 인덱스가 5인 노드의 자리에 31이 들어가도 그 부모 노드인 30보다 크기 때문에 한번 더 반복문을 돌게 된다. 최종적으로 인덱스 2의 자리에 31이 들어가게 된다.
최대 Heap 루트 노드 삭제 연산
: 히프에서는 루트 노드의 원소만 삭제할 수 있다. 루트 노드를 삭제해서 원소의 갯수가 n-1개가 되었으니 완전 이진 트리의 조건에 부합하도록 마지막 노드인 n번째 노드를 지워야 한다. 지우기 전 마지막 노드의 원소를 임시 변수에 저장하고 비어 있는 루트 노드를 채우고 남은 노드들의 위치를 재정립하기 위해 후속처리를 해준다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
int deleteHeap(heapType* h) {
int parent, child;
int item, tmp;
item = h->heap[1];
tmp = h->heap[h->heap_size];
h->heap_size = h->heap_size - 1;
parent = 1;
child = 2;
while(child <= h->heap_size) {
if((child < h->heap_size) && (h->heap[child]) < h->heap[child+1]) child++;
if(tmp >= h->heap[child]) break;
else {
h->heap[parent] = h->heap[child];
parent = child;
child = child*2;
}
}
h->heap[parent] = tmp;
return item;
}
|
cs |
item은 삭제할 루트 노드의 값을 담아 반환하는 변수, tmp는 삭제할 마지막 노드의 원소 값을 임시로 담아두는 변수이다. 각 변수에 그 값을 담아주고 원소의 갯수가 줄어들었으니 heap_size - 1을 해준다. parent와 child는 후속처리를 위한 변수이다.
반복문으로 첫 노드부터 마지막 노드까지 child가 돌아야하기 때문에 조건문은 child <= h->heap_size.
첫번째 if문은, child가 마지막 노드가 아니면서(child < h->heap_size) && child번 째 노드가 child+1번째 노드보다 작다면(h->heap[child] < h->heap[child+1]) child를 1 증가시킨다.
두번째 if문은, tmp의 값이 child번째 노드 보다 크거나 같으면 break
세번째 else, 위 조건 모두 아니면 child번째 노드의 원소를 parent번째 노드에 담고, child의 인덱스가 parent에 담기며, child는 왼쪽 자식 노드로 이동하게 된다.
반복문 종료 후 parent 변수에 알맞은 tmp 위치가 나오면 tmp 값을 담고 루트 노드의 원소가 담겨있던 item을 반환하며 끝.
if문에 대한 이해는 글 보다는 예시와 함께 보면 이해 하기 쉬우므로 밑에 그림으로 한번 더 설명.

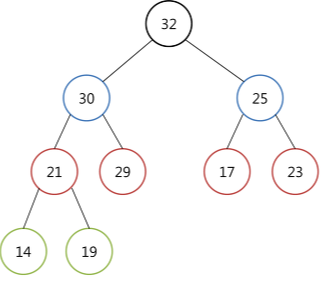
위 최대 히프 트리를 예시로 들어 설명해보자면 item에는 32가 담기고 마지막 노드인 19가 tmp에 담긴다. 배열의 크기는 9이지만 삭제하기 때문에 8이 된다. parent = 1, child = 2의 초기값을 가지고 가기 때문에 parent는 1번째 노드인 32, child는 2번째 노드인 30를 가리킨다.
첫 if문을 만나면 child가 배열의 크기 보다 작지만 child의 원소가 child+1의 원소보다 작지 않기 때문에 조건문을 만족하지 못 한다.
두번째 if문을 만나도 원소가 19인 tmp가 child 노드의 원소인 30보다 크지 않기 때문에 조건문을 만족하지 못 한다.
마지막으로 else로 가서, h->heap[parent] = h->heap[child]를 진행하면 child번째 노드의 값을 1번째 노드에 담는다. 즉, 루트 노드가 30이 된다. 그 후, parent = child, child = child*2로 parent에는 2가 담기고 child에는 child의 왼쪽 자식 노드의 인덱스인 4가 된다.
child가 아직 배열의 크기보다 작기 때문에 계속 반복문을 돌게된다. 하지만 이번에는 child가 child+1보다 작기 때문에 첫 if문을 만족한다. 그렇기에 child++로 child는 5가 된다. child가 5가 되어도 두번째 if문을 만족시키지 못 하기 때문에 다시 반복을 돌게 된다.
child = 5도 두 if문을 만족시키지 못 하고 else로 넘어가게 되어서, 비어있던 parent(=2)번째 노드에 child(=29)가 담기고, parent 값은 5가 되며, child = 10이 되어 배열의 크기보다 커지기 때문에 while문이 종료된다.
반복문 종료 후 heap[parent] = tmp이기 때문에 5번째 노드에 19가 들어가게 된다.
순차 자료구조를 이용한 최대 히프 구현 전체 코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
|
#include <stdio.h>
#include <stdlib.h>
#define MAX_ELEMENT 100
//히프에 대한 1차원 배열과 히프 원소의 갯수를 구조체로 묶어 선언
typedef struct {
int heap[MAX_ELEMENT];
int heap_size;
} heapType;
heapType *createHeap() { //공백 히프를 생성하는 연산
heapType *h = (heapType*)malloc(sizeof(heapType));
h->heap_size = 0;
return h;
}
//히프에 item을 삽입하는 연산
void insertHeap(heapType *h, int item) {
int i;
h->heap_size = h->heap_size + 1;
i = h->heap_size;
while ((i !=1 )&& (item > h->heap[i/2])) {
h->heap[i] = h->heap[i/2];
i /=2;
}
h->heap[i] = item;
}
//히프의 루트 노드를 삭제하여 반환하는 연산
int deleteHeap(heapType* h) {
int parent, child;
int item, tmp;
item = h->heap[1];
tmp = h->heap[h->heap_size];
h->heap_size = h-> heap_size - 1;
parent = 1;
child = 2;
while(child <= h->heap_size) {
if((child < h->heap_size) && (h->heap[child]) < h->heap[child+1]) child++;
if(tmp >= h->heap[child]) break;
else {
h->heap[parent] = h->heap[child];
parent = child;
child = child*2;
}
}
h->heap[parent] = tmp;
return item;
}
|
cs |
참고 : C로 배우는 쉬운 자료구조 / 이지영 / 한빛아카데미
'C' 카테고리의 다른 글
| 신장 트리 / 최소 비용 신장 트리 / 프림 알고리즘, 크루스칼 알고리즘 - C 언어 (0) | 2021.06.10 |
|---|---|
| 그래프의 개념과 구조 - C 언어 (0) | 2021.06.08 |
| 이진 탐색 트리의 탐색/삽입/삭제 연산 - C언어 (1) | 2021.05.30 |
| 트리와 이진트리의 개념과 구조 - C언어 (0) | 2021.05.28 |
| 연결리스트를 이용한 큐의 구현 | 연결큐 - C 언어 (0) | 2021.05.27 |
