https://tildacoderecorder.tistory.com/104
이진 트리에 대한 개념 설명은 아래 글 참조 👇🏻
[ 자료구조 ] 트리와 이진트리의 개념과 구조 - C언어
트리 : 원소들 간에 1:n 관계를 가지는 비선형 자료구조, 원소들 간에 계층 관계를 가지는 계층형 자료구조, 상위 원소에서 하위 원소로 내려가면서 확장되는 트리(나무) 모양의 구조 트리는 하나
tildacoderecorder.tistory.com
이진 탐색 트리 Binary search Tree
: 이진 트리를 탐색용 자료구조로 사용하기 위해 원소 크기에 따라 노드 위치를 정한 것
- 모든 원소는 서로 다른 유일한 키를 갖는다.
- 왼쪽 서브 트리에 있는 원소들의 키는 그 루트의 키보다 작다.
- 오른쪽 서브 트리에 있는 원소들의 키는 그 루트의 키보다 크다.
- 왼쪽 서브 트리와 오른쪽 서브 트리도 이진 탐색 트리이다.
기본 설정
|
1
2
3
4
5
6
7
8
9
10
11
12
|
#include<stdio.h>
#include<stdlib.h>
typedef int element;
typedef struct treeNode {
int key;
struct treeNode* right; //오른쪽 서브 트리
struct treeNode* left; //왼쪽 서브 트리
} treeNode;
|
cs |
이진 탐색 트리의 탐색 연산
: 루트에서부터 시작해 찾고자 하는 키를 루트의 키와 비교해 보다 작다면 왼쪽 서브 트리로 이동, 크다면 오른쪽 서브 트리로 이동해야 한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
treeNode* searchBST(treeNode *root, int x) {
treeNode* p = root;
while ( p != NULL ){
if ( x < p->key ) p = p->left;
else if ( x == p->key ) return p;
else p = p->right;
}
printf("찾는 키가 없습니다!");
return p;
}
|
cs |
탐색 함수의 파라미터는 이진 트리의 root 값과 찾을 키의 값인 x.
먼저 root 값을 treeNode 구조체의 변수 p( 현재 노드라는 의미 )에 담아준다. while문을 이용해 찾고자 하는 키 값을 찾을 때 까지, 또는 찾지 못 해 root값이 NULL이 될 때 까지 반복한다.
if문으로 찾고자 하는 키 x가 현재 노드의 키 값보다 작으면 왼쪽 서브 트리로 이동해야 하므로 p=p->left, 작지 않고 p의 키값과 동일하다면 탐색에 성공한 것이므로 p를 반환하고 종료. 위 두 조건 모두 맞지 않는다면 오른쪽 서브 트리로 이동 p=p->right하며 계속 반복한다.
while문이 끝났는데도 찾지 못 했다면 메세지를 출력하고 마지막으로 탐색이 끝난 노드 P를 리턴하며 종료.
이진 탐색 트리의 삽입 연산
: 먼저 탐색 연산을 수행. 삽입할 원소가 트리에 있으면 삽입할 수 없으므로 같은 원소가 있는지 탐색하여 확인. 탐색 실패한 위치에 알맞게 원소를 삽입.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
treeNode* insertNode(treeNode *p, int x) {
treeNode *new;
if(p==NULL) {
new = (treeNode*)malloc(sizeof(treeNode));
new->key = x;
new->right=NULL;
new->left=NULL;
return new;
}
else if(x<p->key) p->left = insertNode(p->left,x);
else if(x>p->key) p->right = insertNode(p->right,x);
else printf("같은 키 존재");
return p;
}
|
cs |
먼저 노드를 삽입하기 위해 새 노드를 생성한다. treeNode *new
if문을 제치고 밑에 else if를 먼저 보자면, 이 부분은 위의 탐색 연산을 구현한 것이다. x값이 p의 키 값보다 작으면 왼쪽 서브트리로 이동한 값을 파라미터로 넣고 insertNode 함수를 다시 호출한다. 다시 호출된 insertNode 함수 안에서 또 if문과 else if문을 확인하며 x가 p의 키 보다 작거나 크면 위와 같이 함수를 호출하는 방법을 끊임없이 반복, 즉 재귀함수가 되는 것이다.
재귀 함수를 반복하다 첫번째 if문에 부합하면, p==NULL이라면 탐색을 끝마치고 x가 들어갈 알맞은 위치를 찾은 것이기 때문에 새 노드 new의 키 값에 x를 넣어준다.
이진 탐색 트리의 삭제 연산
: 탐색 연산을 통해 삭제해야할 원소가 들어있는 노드의 위치를 찾는다. 노드의 삭제 후에도 이진 트리의 구성을 유지해야하기 때문에 세 가지 경우를 살펴봐야 함. 삭제할 노드가 단말 노드인 경우, 삭제할 노드가 자식 노드를 한 개 가진 경우, 삭제할 노드가 자식 노드를 두 개 가진 경우
전체 코드가 꽤 기므로 세 가지 경우로 나눠서 살펴본다. 먼저 삭제할 노드를 찾기 위해 트리에서 키를 찾는다.
|
1
2
3
4
5
6
7
|
void deleteNode(treeNode *root, element key) {
treeNode *parent, *p, *succ, *succ_parent;
treeNode *child;
parent = NULL;
p = root;
|
cs |
root와 삭제할 key 값을 파라미터로 받는다. ( 코드 맨 첫 줄에 typedef int element로 element를 정수형 타입으로 지정해준다. )
p는 루트를 가리키는 포인터 변수, parent는 p의 부모 노드, child는 p의 자식 노드를 가리킬 포인터 변수이다. 루트는 부모 노드가 없으므로 parent의 초기값은 NULL.
succ는 successor = 후계자의 약자로 succ 변수는 자식 노드를 두 개 가진 경우에 사용할 예정.
삭제할 노드 위치 탐색 + 삭제할 노드가 없는 경우
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
while ((p != NULL) && (p->key != key)) { //삭제할 노드의 위치 탐색
parent = p;
if(key < p->key) p = p->left;
else p = p->right;
}
//삭제할 노드가 없는 경우
if(p == NULL) {
printf("키가 이진 트리에 없음");
return;
}
|
cs |
while문을 돌며 먼저 parent에 p를 넣어주고 key와의 크기 비교를 통해 왼쪽 서브 트리 또는 오른쪽 서브 트리로 이동한 값을 p에 넣어준다.
while의 조건문은 'p가 NULL이면 반복을 종료', 또는 'p의 key값이 삭제할 key값과 동일하면 종료'를 뜻한다.
p의 key 값이 삭제할 key 값과 동일하다면 삭제할 key값이 담긴 노드가 p에 담긴 채 while문이 종료된다. 하지만 p가 NULL이면 찾고자 하는 key값이 트리 자체에 없는 것이므로 에러 메세지를 출력하며 종료한다.
반복문이 끝난 뒤 변수 p에 삭제할 노드의 위치가 담겨있음을 기억하고 아래의 세 가지 경우를 살펴봐야한다.
삭제할 노드가 단말 노드인 경우
|
1
2
3
4
5
6
7
8
9
10
11
12
|
//삭제할 노드가 단말 노드인 경우
if((p->left==NULL) && (p->right==NULL)) {
if(parent != NULL) {
if( parent->left == p) parent->left = NULL;
else parent->right = NULL;
}
else root = NULL;
}
|
cs |
p의 왼쪽 자식 노드와 오른쪽 자식 노드가 모두 NULL이라면 단말 노드이다. 이제 P가 루트인지 아닌지만 살펴보면된다. 루트는 부모 노드가 없으므로 parent = null이다.
if문을 통과해 p가 루트가 아니라면 p가 parent의 왼쪽 자식 노드인지, 오른쪽 자식 노드인지 확인 후 왼쪽 자식 노드라면 parent -> left = NULL로 노드를 삭제하고 오른쪽도 이와 동일하게 진행한다.
만약 if문을 통과하지 못 하고 p가 루트일 때는 루트를 바로 NULL로 만든다.

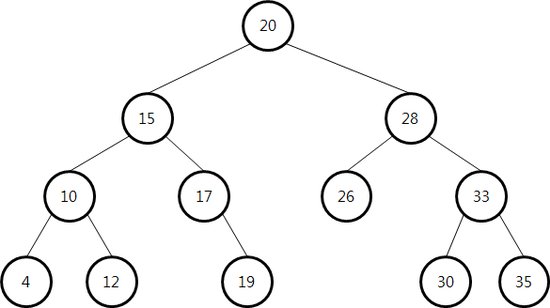
위 트리를 예시로 볼 때, 삭제하고자 하는 노드가 오른쪽 맨 아래인 35라고 가정하자. 35는 자식 노드가 전혀 없는 단말 노드이고 parent는 33이다. 35는 parent의 오른쪽 자식노드이기 때문에 parent->right = NULL하면 35는 삭제된다.
만약 p가 자식 노드가 하나도 없는 루트인 20이라면 루트만 NULL을 만들어주면 된다. ( = 트리에 오직 루트 노드 하나만 있는 경우 )
삭제할 노드가 자식 노드를 한 개 가진 경우
: 자식 노드를 한 개 가지고 있다면 현재 노드 p를 삭제 했을 때 트리가 끊기게 되므로 p의 자식노드를 p의 부모 노드와 이어줘야 한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
//삭제할 노드가 자식 노드를 한 개 가진 경우
else if ((p->left == NULL) || (p->right == NULL)){
if( p->left != NULL) child = p->left;
else child = p->right;
if (parent != NULL) {
if(parent->left == p) parent -> left = child;
else parent -> right = child;
}
else root = child;
}
|
cs |
p의 왼쪽 자식 노드 '또는' 오른쪽 자식 노드 둘 중 하나만 null일 때, p는 한 개의 자식 노드를 갖고 있다.
먼저 p의 자식 노드가 왼쪽인지 오른쪽인지 확인하기 위해 if문을 이용하고 자식 노드 값을 변수 child에 담는다.
그 다음, parent가 null이 아닐 때 ( =노드가 루트가 아닐 때), p의 부모 노드와 자식 노드를 이어줘야 하므로 p가 부모 노드의 왼쪽인지 오른쪽인지 판별 후 child와 연결한다.
만약 p가 단 하나의 루트 노드라면 p는 삭제되고 root값은 p의 자식 노드가 된다.

위 트리를 예시로 설명해보자면, 삭제할 노드는 자식 노드를 1개만 가지고 있어야 하니 17이라고 가정하자. 17의 자식노드는 19이고 19는 오른쪽 자식 노드이며 child는 19가 된다. 17은 부모 노드 15의 오른쪽 자식 노드이므로 부모 노드의 오른쪽이 자식 노드 19와 이어지도록 해야 17을 삭제할 수 있다. parent->right = child
만약 트리에 루트 노드 17 그리고 자식 노드 19 딱 두 노드만 존재했다면, parent = NULL 이기 때문에 root = child로 자식 노드인 19가 루트가 되어 기존 루트인 17은 삭제된다.
삭제할 노드가 자식 노드를 두 개 가진 경우
마지막으로 삭제할 노드가 자식 노드를 두 개 가진 경우이다. 여기서는 후계자 노드 변수인 succ와 후계자 부모 노드 succ_parent를 사용한다.
자식 노드를 가지고 있는 노드를 삭제하면, 그 밑의 자식 노드들은 연결이 끊어지게 된다. 이 때 자식 노드들 중 후계자를 찾아 삭제된 노드의 위치에 넣어주어 연결을 유지하는 후속 처리를 해줘야 한다.

먼저 그림을 보며 설명하자면, 삭제할 노드가 자식 노드를 두 개 가진 경우는 위 트리 중 20, 15, 10, 28, 33이 될 수 있다. 이 중 노드 15를 삭제한다고 가정하자. 15가 삭제된다면 자식 노드인 10과 17 그리고 그 밑에 있는 자식노드들과 루트 20 사이의 연결이 끊어진다.
이 연결을 유지 시키기 위해 자식 노드 사이에서 후계자를 찾아야 하는데 후계자를 찾는 방법에는 두 가지가 있다.
- 왼쪽 자식 노드 중 가장 큰 노드 찾기
- 오른쪽 자식 노드 중 가장 작은 노드 찾기
이 글에서는 첫번째 방법을 선택할 것이다. 두 방법 중 어떤 것을 선택하는지는 자유.
노드 15를 삭제 했을 때 왼쪽 자식 노드 중 가장 큰 값인 12를 15의 자리에 넣게 되면 이진 트리의 조건을 그대로 만족한다. ( = 오른쪽 자식 노드에서 가장 작은 값인 17을 넣어도 만족)
이를 코드로 적어보면 아래와 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
//삭제할 노드가 자식 노드를 두 개 가진 경우
else {
succ_parent = p;
succ = p->left;
//왼쪽 서브 트리에서 후계자 찾기
while(succ->right != NULL) {
succ_parent = succ;
succ = succ->right;
}
if (succ_parent->left == succ) succ_parent->left = succ->left;
else succ_parent->right = succ->left;
p->key = succ->key;
p=succ;
}
|
cs |
먼저 후계자의 부모 변수에 p를 넣어주고, 후계자 노드는 p->left로 왼쪽 자식 노드로 이동한다.
왼쪽 자식 노드 중 가장 큰 값을 찾으려면 계속 오른쪽 간선을 타고 내려가야 하기 때문에 while문을 이용해 후계자 노드 succ의 오른쪽 간선이 null을 가리킬 때 까지 반복한다.
succ->right가 null을 만나 while문이 종료되고 후계자 노드가 succ에 담긴 다면 후계자 노드가 부모 노드의 왼쪽인지 오른쪽인지를 판별한다. ❗️ 이 부분을 이해하기 위해서 생각해봐야 하는 부분이 있다.
|
1
2
|
if (succ_parent -> left == succ) succ_parent -> left = succ->left;
else succ_parent->right = succ->left;
|
cs |
바로 후계자 노드가 자식 노드를 가지고 있을 수 있다는 경우이다. 후계자 노드도 자식 노드를 0개 또는 1개 가질 수 있다. 2개를 가질 수 없는 이유는, 자식 노드가 2개라면 후계자 노드의 오른쪽 자식노드가 존재한다는 뜻이고 이는 왼쪽 서브 트리에서 가장 큰 값이 후계자 노드가 아닌 후계자의 오른쪽 노드가 되기 때문.
후계자 노드의 자식 노드가 0이라면 후계자 노드만 삭제해주면 되지만, 후계자 노드가 왼쪽 자식 노드를 가지고 있다면 후계자 노드를 삭제했을 때 연결이 끊어지므로, 이 부분을 이어주는 후속 처리를 해주어야 한다. 이 후속처리에 대한 부분이 위 코드이다.
코드를 보면, 후계자 노드가 후계자의 부모 노드의 왼쪽 자식일 때, succ_parent->left = succ->left를 해야한다. 후계자의 왼쪽 자식 노드가 부모 노드의 왼쪽 자식 노드가 되도록 이어주는 것이다. 후계자가 단말 노드라 자식 노드가 없다면 succ->left = null이고, 왼쪽 자식 노드가 있다면 그 값이 후계자의 부모 노드와 이어진다.
후계자 노드가 후계자의 부모 노드의 오른쪽 자식노드라고 해도 위와 동일한 과정을 밟는다.
이를 그림으로 보면

후계자 부모 노드, 후계자 노드, 후계자의 자식 노드
1. 후계자 노드가 왼쪽 자식 노드이고, 단말 노드인 경우 : succ->left = null이므로 succ_parent->left=succ->left를 하면 후계자 부모 노드에 null 값만 담김.
2. 후계자 노드가 왼쪽 자식 노드이고, 자식 노드를 하나 가지고 있는 경우 : succ_parent->left = succ->left 후계자 부모 노드와 후계자 자식노드가 이어짐.
3. 후계자 노드가 오른쪽 자식 노드이고, 단말 노드인 경우 : 1번과 동일.
4. 후계자 노드가 오른쪽 자식 노드이고, 자식 노드를 하나 가지고 있는 경우 : 2번과 동일.
후속처리가 끝난 뒤에는 p->key = succ->key로 삭제할 p의 자리에 succ의 키 값을 넣어주고 ( 키값이 바뀌면서 논리적으로 삭제됨), 후계자 노드도 삭제해야 하므로 p가 succ를 가리키도록 한 뒤 free(p)를 해준다.
free(p)는 위 삭제의 세 가지 경우 모두 해당. 아래 전체 코드를 보며 처음부터 끝까지 다시 읽어보는게 이해하기 좋다.
이진 탐색 트리 탐색, 삽입, 삭제 연산 한번에 보기
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
|
#include<stdio.h>
#include<stdlib.h>
typedef int element;
typedef struct treeNode {
int key;
struct treeNode* right; //오른쪽 서브 트리
struct treeNode* left; //왼쪽 서브 트리
} treeNode;
treeNode* searchBST(treeNode *root, int x) {
treeNode* p = root;
while(p != NULL){
if( x < p->key) p = p->left;
else if(x == p->key) return p;
else p = p->right;
}
printf("찾는 키가 없습니다!");
return p;
}
treeNode* insertNode(treeNode *p, int x) {
treeNode *new;
if(p == NULL) {
new = (treeNode*)malloc(sizeof(treeNode));
new->key = x;
new->right=NULL;
new->left=NULL;
return new;
}
else if(x < p->key) p->left = insertNode(p->left,x);
else if(x > p->key) p->right = insertNode(p->right,x);
else printf("같은 키 존재");
return p;
}
void deleteNode(treeNode *root, element key) {
treeNode *parent, *p, *succ, *succ_parent;
treeNode *child;
parent = NULL;
p = root;
while ((p != NULL) && (p->key != key)) { //삭제할 노드의 위치 탐색
parent = p;
if(key < p->key) p = p->left;
else p = p->right;
}
//삭제할 노드가 없는 경우
if(p == NULL) {
printf("키가 이진 트리에 없음");
return;
}
//삭제할 노드가 단말 노드인 경우
if((p->left == NULL) && (p->right == NULL)) {
if(parent != NULL) {
if( parent->left == p) parent->left = NULL;
else parent->right = NULL;
}
else root = NULL;
}
//삭제할 노드가 자식 노드를 한 개 가진 경우
else if ((p->left == NULL) || (p->right == NULL)){
if( p->left != NULL) child = p->left;
else child = p->right;
if (parent != NULL) {
if(parent->left == p) parent -> left = child;
else parent -> right = child;
}
else root=child;
}
//삭제할 노드가 자식 노드를 두 개 가진 경우
else {
succ_parent = p;
succ = p->left;
//왼쪽 서브 트리에서 후계자 찾기
while(succ->right != NULL) {
succ_parent = succ;
succ = succ->right;
}
if (succ_parent -> left == succ) succ_parent -> left = succ->left;
else succ_parent->right = succ->left;
p->key = succ->key;
p=succ;
}
free(p);
}
|
cs |
참고 : C로 배우는 쉬운 자료구조 / 이지영 / 한빛아카데미
'C' 카테고리의 다른 글
| 그래프의 개념과 구조 - C 언어 (0) | 2021.06.08 |
|---|---|
| heap의 개념과 구조, 삽입/삭제 연산 - C언어 (0) | 2021.06.01 |
| 트리와 이진트리의 개념과 구조 - C언어 (0) | 2021.05.28 |
| 연결리스트를 이용한 큐의 구현 | 연결큐 - C 언어 (0) | 2021.05.27 |
| enQueue( )와 deQueue( ) 함수를 이용한 원형큐 - C 언어 (0) | 2021.05.26 |