문제
재원이는 한 도시의 시장이 되었다. 이 도시에는 도시를 동쪽과 서쪽으로 나누는 큰 일직선 모양의 강이 흐르고 있다. 하지만 재원이는 다리가 없어서 시민들이 강을 건너는데 큰 불편을 겪고 있음을 알고 다리를 짓기로 결심하였다. 강 주변에서 다리를 짓기에 적합한 곳을 사이트라고 한다. 재원이는 강 주변을 면밀히 조사해 본 결과 강의 서쪽에는 N개의 사이트가 있고 동쪽에는 M개의 사이트가 있다는 것을 알았다. (N ≤ M)
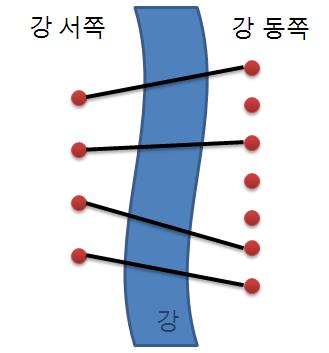
재원이는 서쪽의 사이트와 동쪽의 사이트를 다리로 연결하려고 한다. (이때 한 사이트에는 최대 한 개의 다리만 연결될 수 있다.) 재원이는 다리를 최대한 많이 지으려고 하기 때문에 서쪽의 사이트 개수만큼 (N개) 다리를 지으려고 한다. 다리끼리는 서로 겹쳐질 수 없다고 할 때 다리를 지을 수 있는 경우의 수를 구하는 프로그램을 작성하라.
입력
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 강의 서쪽과 동쪽에 있는 사이트의 개수 정수 N, M (0 < N ≤ M < 30)이 주어진다.
출력
각 테스트 케이스에 대해 주어진 조건하에 다리를 지을 수 있는 경우의 수를 출력한다.
| 예제 입력 1 | 예제 출력 1 |
| 3 2 2 1 5 13 29 |
1 5 67863915 |
조건을 살펴보면
- N은 0 보다 큰 정수이고, M은 N보다 크거나 같으면서 30 이하여야 한다.
- 다리를 N개만큼 짓기 때문에 N과 M이 짝지어질 때 N은 무조건 짝이 있어야 하지만 M은 짝이 없어 남는 숫자가 있어도 된다(M이 N보다 같거나 크기 때문에).
- 다리끼리는 서로 겹쳐질 수 없기 때문에 N과 짝지어질 M은 이전 경우의 수보다 큰 수여야한다. 예를 들어 N이 2, M이 3일 때 만들 수 있는 다리의 수는 ([1, 1], [2, 2]), ([1, 1], [2, 3]), ([1, 2], [2, 3]) 와 같이 3가지이며 M은 이전 경우에서 N과 짝지은 수보다 커야함을 알 수 있다.
📍 결론 : M개의 숫자 중에서 N개를 고르는 경우의 수를 중복 없이 찾으면 된다.
위 예시에서 설명했듯이 N이 2, M이 3일 때 둘을 짝짓는 경우의 수를 구하면
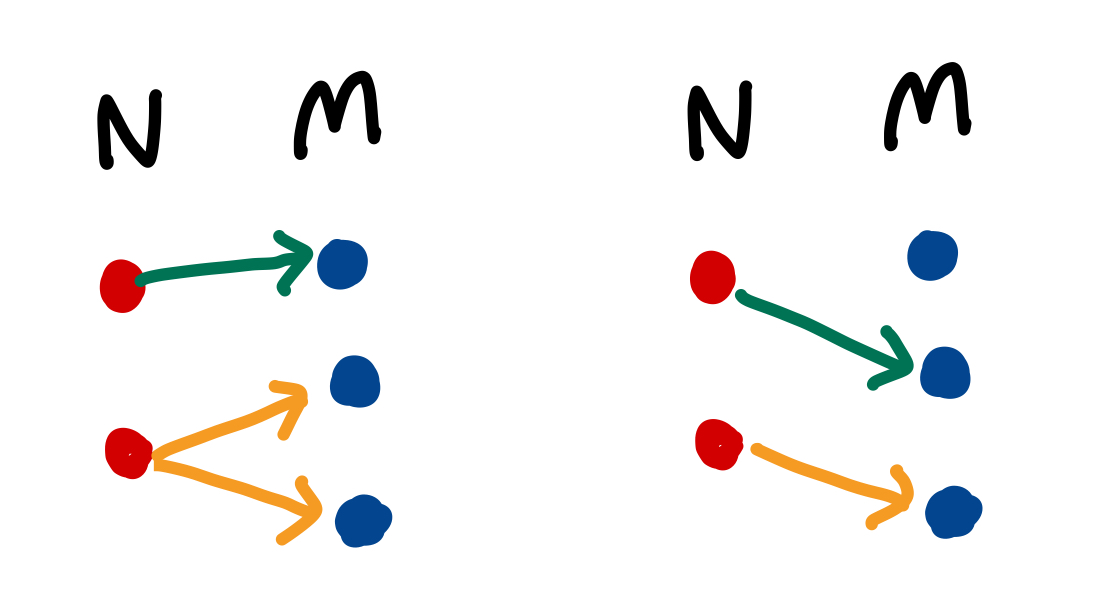
N의 1이 M의 1과 짝을 맺는 경우 N의 2는 M의 2, 3과 짝을 맺을 수 있다.
[1, 1], [2, 2]
[1, 1], [2, 3]
다음으로 N의 1이 M의 2와 짝을 맺는 경우 N의 2는 M의 3이랑만 짝을 맺을 수 있다.
[1, 2], [2, 3]
다리가 겹치면 안되기 때문에 [1, 1], [2, 1]이나 [1, 2], [2, 2] 와 같은 조합은 나올 수 없다.
따라서 경우의 수는 3가지이다.
재귀 함수 풀이
import java.util.*;
public class Main {
public static int countPair(int n, int m){
if(n==0){
return 1;
}
int count = 0;
for(int i = n; i<=m; i++){
count += countPair(n-1, i-1);
}
return count;
}
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
for(int i=0; i<t; i++){
int n = sc.nextInt();
int m = sc.nextInt();
System.out.println(countPair(n, m));
}
}
}
경우의 수를 구하는거니까 재귀함수를 사용했다.
※ 재귀함수란 함수가 자기 자신을 다시 호출하는 것을 뜻한다. 이러한 재귀 함수는 자신의 로직을 내부적으로 반복하다가 일정 조건이 만족되면 함수를 이탈하여 결과를 호출한다.
👇🏻 재귀 함수 풀이 설명
N=3, M=5 라고 가정할 때
countPair( ) 함수에 3과 5가 들어가면 for문을 타고
count += countPair(2, 2)
count += countPair(2, 3)
count += countPair(2, 4)
를 각각 호출한다.
countPair(2, 2)는 또 다시 for문을 타고
countPair(1, 1)를 호출하고 이 함수 또한 for문을 타고
countPair(0, 0)를 호출하게 되는데 이는 첫번째 If문의 조건 n==0을 만족하기 때문에 1을 반환하고 함수가 종료된다.
countPair(2, 3)은 위와 같은 방법으로
countPair(1, 1) countPar(1, 2)를 호출하게 되고 이 두 함수는 각각
countPair(0, 0) 과 countPair(0, 1) countPair(0, 2)를 호출하게 되는데
모두 n==0을 만족하므로 각각 1을 반환하고 함수가 종료된다. (총 3 함수가 1을 반환하기 때문에 결론적으로 3이 반환됨)
countPair(2, 4)도 위와 같은 재귀 함수의 로직을 이용하면 6을 반환하고 종료된다.
따라서 이 셋의 경우의 수를 모두 더한 10이 답이 된다.

그런데 제출하니까 시간 초과가 떠서 다른 방법을 알아봐야했다.
조합 알고리즘 풀이
import java.util.*;
public class Main {
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
for(int i=0; i<t; i++){
int n = sc.nextInt();
int m = sc.nextInt();
int result = 1;
for(int j=0; j<n ; j++){
result = result*(m-j)/(j+1);
}
System.out.println(result);
}
}
}
M개의 숫자 중에서 N개를 고르는 경우의 수는 조합 알고리즘 mCn( m Combination n )을 사용해 구할 수 있다.
mCn = m! / n! (m-n)!
mCn의 공식은 위와 같다.
m이 n보다 같거나 큰 숫자이므로 분자의 m! 은 m * (m-1) * (m-2) * ... * n * (n-1) * (n-2) *...2 * 1 임을 알 수 있는데 이는 분모의 (m-n)! 로 약분이 된다. ex) m이 5 n이 3일 때 5!는 5*4*3*2*1이므로 (m-n)!인 2*1을 포함하기에 약분하면 5*4*3이 남는다.
따라서 분자에는 m부터 n까지의 수를 차례대로 곱한 값이 들어가고 분모에는 n!, 즉 1부터 n까지의 곱셈 값이 들어가게 된다.
이를 위 문제와 더해 코드로 구현하면 아래와 같다.
int result = 1;
for(int j=0; j<n ; j++){
result = result*(m-j)/(j+1);
}
'코테 문제 풀이 > 백준' 카테고리의 다른 글
| 백준 - 2179번 : 비슷한 단어 Java (0) | 2024.09.26 |
|---|